자료 구조 - 복잡도
자료 구조(data structure)란?
효율적으로 데이터를 관리하고 수정, 삭제, 탐색, 저장할 수 있는 데이터 집합을 말합니다.
복잡도는 시간 복잡도와 공간 복잡도로 나뉩니다.
시간 복잡도(Time Complexity)
시간 복잡도는 알고리즘이 수행되는 데 걸리는 시간을 입력 크기와 관련하여 분석하는 방법입니다. 알고리즘의 성능을 측정할 떄 입력 크기 n에 따라 실행 시간이 얼마나 빠르게 증가하는지를 나타냅니다. 이를 빅오 표기법(Big-O Notation)으로 나타내어, 최악의 경우에 알고리즘이 얼마나 많은 작업을 수행해야 하는지 설명합니다.
빅오 표기법(Big-O Notation)
빅오 표기법은 알고리즘의 성능을 추상적으로 표현하며, 입력이 증가함에 따랄 알고리즘의 실행 시간이 얼마나 변하는지를 나타냅니다. 빅오 표기법에서 상수 시간은 무시되고, 입력 크기 n에 의한 주요 성능 변화를 나타내는 지수만 고려됩니다.
자주 사용되는 시간 복잡도 종류
O(1) (상수 시간): 입력 크기에 상관없이 항상 일정한 시간이 걸리는 알고리즘입니다.
• 예: 배열에서 첫 번째 원소를 조회하는 경우.
• 예시: int first = arr[0];
O(log n) (로그 시간): 입력 크기가 커질수록 시간이 느리게 증가하는 경우로, 보통 이진 탐색에서 발생합니다.
• 예: 정렬된 배열에서 이진 탐색으로 값을 찾을 때.
• 예시: 이진 탐색 알고리즘
O(n) (선형 시간): 입력 크기에 비례하여 시간이 증가합니다. 즉, 입력 크기가 커지면 수행 시간도 그만큼 증가하는 알고리즘입니다.
• 예: 배열에서 최대값을 찾기 위해 모든 요소를 한 번씩 확인하는 경우.
• 예시: for (int i = 0; i < n; i++) { ... }
O(n log n): 퀵 정렬이나 병합 정렬 같은 효율적인 정렬 알고리즘에서 자주 등장하는 시간 복잡도입니다. 정렬 작업은 대체로 O(n log n)의 시간 복잡도를 가집니다.
• 예: 병합 정렬, 퀵 정렬
• 예시: 정렬 알고리즘 구현
O(n^2) (이차 시간): 중첩된 반복문이 있을 때 발생하며, 입력 크기가 커질수록 시간이 제곱 비율로 증가합니다.
• 예: 두 배열에서 모든 조합을 비교하거나, 버블 정렬 같은 비효율적인 정렬 알고리즘에서 발생.
• 예시: for (int i = 0; i < n; i++) { for (int j = 0; j < n; j++) { ... } }
O(2^n) (지수 시간): 재귀적으로 분기하여 모든 경우의 수를 탐색하는 알고리즘에서 발생합니다. 입력 크기가 조금만 커져도 실행 시간이 급격하게 증가합니다.
• 예: 피보나치 수열을 재귀적으로 계산하는 경우, 모든 부분집합을 구하는 알고리즘
• 예시: fibonacci(n) = fibonacci(n-1) + fibonacci(n-2);
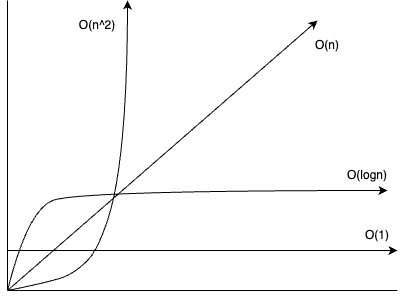
앞의 그림처럼 O(1)과O(n)입력 크기가 커질수록 차이가 많이 나는 것을 볼 수 있습니다. O(n^2)은 말할 것도 없을 만큼 차이가 크다. 즉 O(n^2)보다는 O(n), O(n)보다는 O(1)을 지양해야 합니다.
예시로 살펴보기
배열에서 최대값 찾기
• 배열에 있는 요소들을 하나씩 비교해서 가장 큰 값을 찾는 알고리즘입니다.
• 시간 복잡도는 O(n)입니다. 왜냐하면, 배열의 모든 요소를 한 번씩 비교해야 하기 때문에, 입력 크기 n 에 비례하는 시간이 필요합니다.
이진 탐색(Binary Search)
• 정렬된 배열에서 중간 값을 선택하여 찾고자 하는 값과 비교한 후, 값을 절반으로 줄여가는 방식입니다.
• 시간 복잡도는 O(log n)입니다. 배열의 길이가 절반씩 줄어들기 때문에, 비교 횟수는 로그에 비례하여 감소합니다.
동작 원리
- 배열의 중간 값을 선택하여 찾고자 하는 값과 비교합니다.
- 찾고자 하는 값이 중간 값보다 크면, 배열의 오른쪽 절반에서 다시 탐색을 진행하고, 중간 값보다 작으면 왼쪽 절반에서 탐색을 진행합니다.
- 이 과정을 반복하여 범위를 절반씩 줄여가면서 값을 찾습니다.
시간 복잡도
최선, 평균, 최악: O(log n)
입력 크기가 n일 때, 비교 횟수는 log_2(n)에 비례하여 줄어듭니다.
예시 코드(자바)
public int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2; // 중간 위치 계산
if (arr[mid] == target) {
return mid; // 값을 찾은 경우
}
if (arr[mid] < target) {
left = mid + 1; // 오른쪽 절반 탐색
} else {
right = mid - 1; // 왼쪽 절반 탐색
}
}
return -1; // 값을 찾지 못한 경우
}
특징을 보면
필수 조건: 배열이 반드시 정렬되어 있어야 합니다.
데이터가 커질수록 효율적인 탐색이 가능하지만, 정렬되지 않은 데이터에는 적용할 수 없습니다.
퀵 정렬(Quick Sort)
퀵 정렬은 분할 정복(Divide and Conquer) 알고리즘의 대표적인 예입니다. 피벗(pivot)을 기준으로 데이터를 두 그룹으로 나누고, 재귀적으로 각 그룹을 정렬하는 방식입니다. 평균적으로 매우 빠른 성능을 보이는 정렬 알고리즘입니다.
동작 원리
- 배열에서 임의의 값을 피벗으로 선택합니다.
- 피벗보다 작은 값들을 피벗의 왼쪽으로, 큰 값들은 피벗의 오른쪽으로 이동시킵니다.
- 피벗을 기준으로 두 부분 배열로 나누고, 각각에 대해 재귀적으로 퀵 정렬을 수행합니다.
시간 복잡도
최선, 평균: O(n log n)
최악: O(n^2) (피벗을 항상 최악의 값을 선택할 경우)
예시 코드
public void quickSort(int[] arr, int low, int high) {
if (low < high) {
int pi = partition(arr, low, high); // 피벗 위치
quickSort(arr, low, pi - 1); // 피벗 왼쪽 정렬
quickSort(arr, pi + 1, high); // 피벗 오른쪽 정렬
}
}
private int partition(int[] arr, int low, int high) {
int pivot = arr[high]; // 마지막 값을 피벗으로 선택
int i = low - 1; // 피벗보다 작은 값들의 경계
for (int j = low; j < high; j++) {
if (arr[j] < pivot) {
i++;
swap(arr, i, j); // 피벗보다 작은 값은 왼쪽으로 보냄
}
}
swap(arr, i + 1, high); // 피벗을 중간에 배치
return i + 1;
}
private void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
특징
빠른 정렬: 평균적으로 O(n log n) 시간 복잡도를 보이며, 실제 사용에서도 매우 효율적입니다.\
최악의 경우: 피벗 선택이 매번 최악일 경우 O(n^2) 시간이 걸릴 수 있지만, 이를 방지하기 위해 랜덤 피벗 선택 등의 최적화 방법을 사용합니다.
병합 정렬(Merge Sort)
병합 정렬도 분할 정복(Divide and Conquer) 기법을 사용하는 정렬 알고리즘입니다. 배열을 반으로 나누고, 각각 재귀적으로 정렬한 후, 두 배열을 병합하여 전체를 정렬합니다.
동작 원리
1. 배열을 더 이상 나눌 수 없을 때까지 절반으로 나눕니다.
2. 나누어진 작은 배열을 정렬한 후, 두 배열을 하나로 병합합니다.
3. 병합된 배열을 다시 병합하는 과정을 반복하여 최종적으로 정렬된 배열을 만듭니다.
시간 복잡도
- 최선, 평균, 최악: O(n log n)
- O(n log n)의 시간 복잡도를 유지합니다.
예시코드
public void mergeSort(int[] arr, int left, int right) {
if (left < right) {
int mid = (left + right) / 2;
mergeSort(arr, left, mid); // 왼쪽 절반 정렬
mergeSort(arr, mid + 1, right); // 오른쪽 절반 정렬
merge(arr, left, mid, right); // 병합
}
}
private void merge(int[] arr, int left, int mid, int right) {
int n1 = mid - left + 1;
int n2 = right - mid;
int[] L = new int[n1];
int[] R = new int[n2];
for (int i = 0; i < n1; i++) {
L[i] = arr[left + i];
}
for (int i = 0; i < n2; i++) {
R[i] = arr[mid + 1 + i];
}
int i = 0, j = 0, k = left;
while (i < n1 && j < n2) {
if (L[i] <= R[j]) {
arr[k] = L[i];
i++;
} else {
arr[k] = R[j];
j++;
}
k++;
}
while (i < n1) {
arr[k] = L[i];
i++;
k++;
}
while (j < n2) {
arr[k] = R[j];
j++;
k++;
}
}
특징
- 안정적인 정렬: 병합 정렬은 안정 정렬입니다. 동일한 값의 원소들의 상대적인 순서는 유지됩니다.
- 일관된 성능: 최선, 평균, 최악의 경우에 모두 O(n log n)의 성능을 보입니다.
- 추가 메모리 필요: 병합 정렬은 추가 메모리 공간을 사용하기 때문에 메모리 사용량이 더 큽니다.
버블 정렬(Bubble Sort)
개요
버블 정렬은 가장 간단한 정렬 알고리즘 중 하나로, 배열에서 인접한 두 원소를 비교하여 큰 값을 오른쪽으로 이동시키는 방식입니다. 이러한 과정을 여러 번 반복하여 전체 배열을 정렬합니다.
동작 원리
1. 배열의 첫 번째 원소부터 인접한 두 원소를 비교합니다.
2. 큰 값을 오른쪽으로, 작은 값을 왼쪽으로 이동시키며, 마지막까지 비교를 반복합니다.
3. 한 번의 반복이 끝나면 가장 큰 값이 배열의 끝에 위치하게 됩니다.
4. 이 과정을 배열이 정렬될 때까지 반복합니다.
시간 복잡도
• 최선: O(n) (이미 정렬된 경우)
• 최악, 평균: O(n^2)
최악, 평균, 최선 시간 복잡도
시간 복잡도는 주로 최악의 경우를 분석하지만, 일부 알고리즘은 최선과 평균에 대한 분석도 필요합니다.
• 최악의 경우 시간 복잡도: 알고리즘이 처리해야 할 입력이 가장 나쁜 경우.
• 최선의 경우 시간 복잡도: 알고리즘이 처리해야 할 입력이 가장 좋은 경우.
• 평균 시간 복잡도: 모든 경우를 평균 내었을 때의 시간 복잡도.
예시 코드
public void bubbleSort(int[] arr) {
int n = arr.length;
boolean swapped;
for (int i = 0; i < n - 1; i++) {
swapped = false;
for (int j = 0; j < n - i - 1; j++) {
if (arr[j] > arr[j + 1]) {
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
swapped = true;
}
}
if (!swapped) break; // 정렬 완료 시 반복 종료
}
}
특징
- 간단한 구현: 버블 정렬은 알고리즘의 동작 방식이 매우 직관적이며 구현하기 쉽습니다. 인접한 두 원소를 비교하여 큰 값을 오른쪽으로 이동시키는 방식이 반복될 뿐입니다.
- 비효율성: 버블 정렬은 인접한 원소들만을 교환하면서 정렬을 진행하기 때문에, 효율성이 떨어집니다. 큰 데이터셋에서는 다른 정렬 알고리즘에 비해 매우 비효율적입니다.
- 비교 기반 정렬: 버블 정렬은 원소들을 비교하여 정렬하는 비교 기반 정렬 알고리즘입니다. 모든 두 원소를 비교하며, 큰 값이 뒤로 이동하도록 정렬합니다.
공간복잡도(Space Complexity)
공간 복잡도는 알고리즘이 실행될 때 사용하는 메모리 양을 입력 크기와 관련하여 측정합니다. 공간 복잡도의 알고리즘이 사용하는 고정된 메모리 양(상수 공간)과 입력 크기에 따라 추가로 필요한 메모리 양(가변 공간)이 포함됩니다.
상수 공간O(1)
상수 공간을 사용하는 알고리즘은 입력 크기와 무관하게 일정한 양의 메모리를 사용합니다.
예시: 두 개의 변수에 값을 저장하고 계산하는 알고리즘
int a = 5;
int b = 10;
int sum = a + b;
재귀 함수와 공간 복잡도
재귀 함수는 호출될 때마다 스택에 저장되므로, 재귀 호출 깊이에 따라 공간 복잡도가 결정됩니다. 예를 들어, 피보나치 수열을 재귀적으로 구현하면, 재귀 호출 스택에 저장되는 함수의 수에 비례하여 메모리가 필요합니다.
예시: 피보나치 수열을 재귀적으로 계산하는 함수는 O(n)의 공간 복잡도를 가집니다.
int fibonacci(int n) {
if (n <= 1) return n;
return fibonacci(n - 1) + fibonacci(n - 2);
}
시간 복잡도와 공간 복잡도의 균형
알고리즘을 최적화 할 때는 시간 복잡도와 공간 복잡도 사이의 균형을 고려해야 한다. 예를 들어, 더 빠른 알고리즘을 구현하기 위해 메모리를 더 많이 사용하는 방법(메모리-시간 트레이드 오프)을 선택할 수도 있습니다.
- 메모리-시간 트레이드 오프(Memory-Time Tradeoff): 알고리즘의 성능을 최적화할 때 사용하는 중요한 개념으로, 메모리 사용량과 실행 시간 사이의 균형을 맞추는 방법을 의미합니다. 일반적으로 알고리즘에서 더 많은 메모리를 사용하면 실행 시간을 줄일 수 있고, 반대로 메모리를 덜 사용하면 실행 시간이 늘어날 수 있습니다.
요약하자면
- 시간 복잡도는 입력 크기 n에 따라 알고리즘이 얼마나 빨리 동작하는지를 분석합니다. 일반적으로 빅오 표기법을 통해 나타내며, 알고리즘이 처리해야 할 작업의 양을 예측합니다.
- 공간 복잡도는 입력 크기 n에 따라 알고리즘이 얼마나 많은 메모리를 사용하는지를 분석합니다. 이를 통해 메모리 사용량을 최적화할 수 있습니다.
자료 구조에서의 시간 복잡도
🔽자료 구조의 평균 시간 복잡도
| 자료 구조 | 접근 | 탐색 | 삽입 | 삭제 |
| 배열(array) | O(1) | O(n) | O(n) | O(n) |
| 스택(stack) | O(n) | O(n) | O(1) | O(1) |
| 큐(queue) | O(n) | O(n) | O(1) | O(1) |
| 이중 연결 리스트(doubly linked list) | O(n) | O(n) | O(1) | O(1) |
| 해시 테이블(hash table) | O(1) | O(1) | O(1) | O(1) |
| 이진 탐색 트리(BST) | O(logn) | O(logn) | O(logn) | O(logn) |
| AVL 트리 | O(logn) | O(logn) | O(logn) | O(logn) |
| 레드 블랙 트리 | O(logn) | O(logn) | O(logn) | O(logn) |
🔽자료 구조 최악의 시간 복잡도
| 자료 구조 | 접근 | 탐색 | 삽입 | 삭제 |
| 배열(array) | O(1) | O(n) | O(n) | O(n) |
| 스택(stack) | O(n) | O(n) | O(1) | O(1) |
| 큐(queue) | O(n) | O(n) | O(1) | O(1) |
| 이중 연결 리스트(doubly linked list) | O(n) | O(n) | O(1) | O(1) |
| 해시 테이블(hash table) | O(1) | O(1) | O(1) | O(1) |
| 이진 탐색 트리(BST) | O(logn) | O(logn) | O(logn) | O(logn) |
| AVL 트리 | O(logn) | O(logn) | O(logn) | O(logn) |
| 레드 블랙 트리 | O(logn) | O(logn) | O(logn) | O(logn) |